Con il
doodle di oggi,
Google celebra il 410° anniversario della nascita dell'illustre matematico e magistrato francese
Pierre de Fermat. Il disegno schematizza l'apparentemente semplice enunciato del celeberrimo
ultimo teorema di Fermat, secondo cui non esistono soluzioni intere positive dell'equazione
an + bn = cn, se
n > 2. Cliccando sul logo Google propone i risultati relativi alla chiave di ricerca
Pierre de Fermat, mentre, passando il cursore del mouse sopra il doodle, compare la scritta «
Dispongo di una meravigliosa dimostrazione di questo teorema, ma questo doodle è troppo piccolo per contenerla», che altro non è se non una spiritosa parafrasi della frase «
Dispongo di una meravigliosa dimostrazione di questo teorema, che non può essere contenuta nel margine troppo stretto della pagina», annotata dallo stesso Fermat a margine di una copia dell'
Arithmetica di
Diofanto sulla quale lui era solito formulare molte delle sue teorie. In effetti, della sua congettura Fermat non lasciò alcuna dimostrazione. Sono dovuti trascorrere circa tre secoli e mezzo, costellati dai vani tentativi di generazioni di matematici... finché nel 1994 il britannico
Andrew Wiles, dopo essersi dedicato per sette interi anni al problema, non è riuscito a venirne a capo: da allora ci si può riferire all'ultimo teorema di Fermat come al
teorema di Fermat-Wiles. Alla sua avvincente storia il divulgatore scientifico
Simon Singh ha dedicato nel 1998 un famoso
saggio... e mentre scrivevo questo post mi è venuta un'incontenibile curiosità di leggerlo!

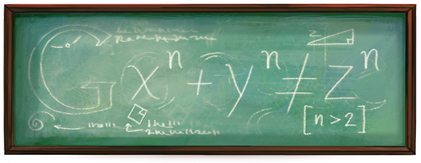

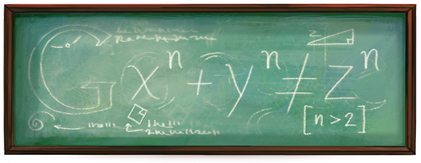

Le mie conclusioni sul teorema di Fermat
RispondiEliminaIl teorema può essere espresso in maniera equivalente nel seguente modo:
se x^n + y^n = z^n per n intero positivo >2 allora x, y,z non possono essere tutti e tre numeri interi positivi.
Dimostrazione
L’equazione descrive un triangolo rettangolo di lati x^(n/2), y^(n/2), z^(n/2). Se x y z fossero tutti e tre interi positivi ,soddisfacendo per ipotesi l’equazione e quindi risolvendo il triangolo, per l’ ipotesi si avrebbe x^n +y^n= z^n e per Pitagora x^2+y^2=z^2 Ma ciò è assurdo in quanto moltiplicando ambo i membri di quest’ultima relazione per z^(n-2) si ottiene x^2*z^(n-2)>x^n+ Y^2*z^(n-2)> y^ n = z^n. dove il primo membro è chiaramente > di x^n+ y^n contrariamente all’ipotesi.
E' sbagliata non se ne tenga conto
EliminaLe
RispondiEliminad'altra parte poiché la soluzione di un triangolo è unica, occorre che la triade (x^(n/2), y^(n/2), z^(n/2) ) soddisfi l’equazione iniziale. Ma allora tale equazione diverrebbe x^((n^2)/2) + y^((n^2)/2)= z^((n^2)/2) dove (((n^2)/2) = n solo se n=2
Non è esatta non se ne tenga conto.
Eliminaavevo concepito per la verità anche quest'altra dimostrazione:
RispondiElimina1. Data l’ipotesi con n primo>2 e x,y,z,interi positivi e coprimi (ogni esponente intero positivo infatti, che non sia 4 o multiplo di 4 può ottenersi dal prodotto di un conveniente numero intero positivo per un determinato primo >2), sia (x,y,z) la terna primitiva minore tale per cui si abbia x^n+y^n=z^n. Tale equazione è l’espressione di un triangolo rettangolo di lati x^(n/2), y^(n/2), z^(n/2); numeri che risolvendo il triangolo, debbono necessariamente soddisfare l’equaz. E poiché un triangolo ha un’unica soluzione e la triade per ipotesi deve essere costituita da numeri interi positivi, occorrerà porre:
x=b^2, y=c^2 z=q^2 dove b,c,q sono evidentemente ancora coprimi,e dove poniamo b e quindi x dispari ( non è riduttivo perché essendo coprimi, due di essi dovranno essere dispari). Allora l’equazione diventa b^(2n)+c^(2n)=q^(2n) cioè:
(q^n-c^n)*(q^n+c^n)=b^(2n)=x^n, dove i due fattori a primo membro sono potenze di grado n perché primi tra loro,essendo q e c coprimi uno pari e l’altro dispari. Cioè q^n+c^n=l^n< x^n<z^n. con l fattore di x e con (q,c,l) terna inferiore a (x,y,z) contrariamente all’ipotesi.
Dunque per i valori ipotizzati (interi positivi) l’equazione non ammette soluzioni, tranne la banale x=y=z=0.
confermo questa
Eliminao se si vuole anche così ( per esere più preciso nei termini):
RispondiEliminaLe mie conclusioni sul teorema di Fermat
Il teorema può essere espresso in maniera equivalente nel seguente modo:
se x^n + y^n = z^n per n intero positivo >2 allora x, y,z non possono essere tutti e tre numeri interi positivi.
Dimostrazione
L’equazione è anche quella di un triangolo rettangolo di lati x^(n/2), y^(n/2), z^(n/2). Se x y z fossero tutti e tre interi positivi ,soddisfacendo l’equazione risolverebbero anche il triangolo. Ma allora per l’ ipotesi si avrebbe x^n +y^n= z^n e per Pitagora x^2+y^2=z^2 Ma ciò è assurdo in quanto moltiplicando ambo i membri di quest’ultima relazione per z^(n-2) si ottiene x^2*z^(n-2)>x^n+ Y^2*z^(n-2)> y^ n = z^n. dove il primo membro è chiaramente > di x^n+ y^n contrariamente all’ipotesi
D’altra parte poiché la soluzione di un triangolo è unica, occorre che la triade (x^ (n/2), y^(n/2), z^(n/2) ) soddisfi l’equazione iniziale. Ma allora tale equazione diverrebbe x^((n^2)/2) + y^((n^2)/2)= z^((n^2)/2) dove (((n^2)/2) = n solo se n=2. Oppure moltiplicando ambo i membri di x^n+y^n=z^n per z^((n^2-2n)/2)) si trova:
x^n*z^((n^2-2n)/2))> x^((n^2)/2)+ y^n*z^((n^2-2n)/2))> y^((n^2)/2)= z^((n^2)/2) che contraddice x^((n^2)/2)+y^((n^2)/2)= z^((n^2)/2)
E'sbagliata non se ne tenga conto.
RispondiElimina